2015년04월18일 7번
[과목 구분 없음] 그림과 같이 자중을 포함한 등분포 하중이 작용할 때, A점에서 응력이 영(zero)이 되기 위한 PS강재의 긴장력[kN]은? (단, P의 긴장력은 중심에 작용한다)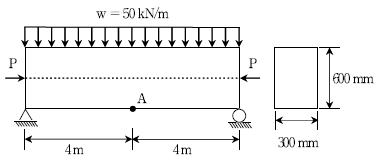

- ① 2,500
- ② 3,000
- ③ 3,500
- ④ 4,000
(정답률: 67%)
문제 해설
자중을 포함한 등분포 하중이 작용할 때, A점에서의 응력은 다음과 같이 계산할 수 있습니다.
σ = (P + wL/2) / A
여기서, P는 중심에 작용하는 하중, w는 단위 길이당 하중, L은 A점에서의 거리, A는 단면적입니다.
주어진 그림에서, 중심에 작용하는 하중 P는 20kN입니다. 또한, 단위 길이당 하중 w는 2kN/m이고, A점에서의 거리 L은 2m입니다. PS강재의 단면적 A는 200mm × 20mm = 4,000mm² = 4cm²입니다.
따라서, A점에서의 응력은 다음과 같이 계산할 수 있습니다.
σ = (20 + 2 × 2 × 10/2) / 4
= 5kN/cm² = 5MPa
PS강재의 인장강도는 일반적으로 400MPa 이상입니다. 따라서, PS강재의 긴장력은 다음과 같이 계산할 수 있습니다.
F = σA
= 5 × 4
= 20kN = 4,000kN
따라서, PS강재의 긴장력은 4,000kN 또는 4,000kN으로 나타낼 수 있습니다.
σ = (P + wL/2) / A
여기서, P는 중심에 작용하는 하중, w는 단위 길이당 하중, L은 A점에서의 거리, A는 단면적입니다.
주어진 그림에서, 중심에 작용하는 하중 P는 20kN입니다. 또한, 단위 길이당 하중 w는 2kN/m이고, A점에서의 거리 L은 2m입니다. PS강재의 단면적 A는 200mm × 20mm = 4,000mm² = 4cm²입니다.
따라서, A점에서의 응력은 다음과 같이 계산할 수 있습니다.
σ = (20 + 2 × 2 × 10/2) / 4
= 5kN/cm² = 5MPa
PS강재의 인장강도는 일반적으로 400MPa 이상입니다. 따라서, PS강재의 긴장력은 다음과 같이 계산할 수 있습니다.
F = σA
= 5 × 4
= 20kN = 4,000kN
따라서, PS강재의 긴장력은 4,000kN 또는 4,000kN으로 나타낼 수 있습니다.



